In questa pagina si riportano 10 quiz svolti di Matematica presenti nei Test Architettura Ufficiali degli scorsi anni.
Quiz n. 1
Traccia:
Se il seno di un angolo ottuso è uguale a 4/5, allora il suo coseno vale:
a) -3/5
b) 3/5
c) -2/5
d) -1/5
e) 1/5
Risoluzione:
Essendo sen(x) noto, si può ricavare cos(x) dalla I relazione fondamentale della goniometria:
Si ha infatti:
⇓
cos(x) = √[1 - (4/5)2]
⇓
cos(x) = √(1 - 16/25)
⇓
cos(x) = √(9/25)
⇓
cos(x) = ±3/5
Poichè l'angolo "x" incognito è ottuso, il suo coseno deve essere necessariamente negativo:
La risposta corretta è, quindi, la a).
Quiz n. 2
Traccia:
Il valore massimo assunto dalla funzione y = –x2 + 5x – 4 è:
a) 4
b) 1
c) + ∞
d) 9/4
e) 5/2
Risoluzione:
Si calcola inizialmente la derivata prima della funzione assegnata:
Si ricava successivamente l'ascissa del punto di massimo imponendo che la derivata prima sia nulla:
⇓
-2x + 5 = 0
⇓
x = 5/2
Il valore massimo assunto dalla funzione corrisponde all'ordinata del punto di massimo; tale valore si ottiene sostituendo il valore della "x" appena ricavato nella funzione iniziale:
⇓
y(5/2) = - (25/4) + (25/2) - 4
⇓
y(5/2) = 9/4
La risposta corretta è, quindi, la d).
Quiz n. 3
Traccia:
Le soluzioni della disequazione (2 – x)(x + 1)x < 0 sono:
a) x < -1 oppure 0 < x < 2
b) -1 < x < 0 oppure x > 2
c) -1 < x < 0
d) x > 2
e) 0 < x < 1 oppure x > 2
Risoluzione:
Si impone inizialmente la positività dei 3 fattori presenti nel I membro della disequazione:
⇓
x < 2
2) x + 1 > 0
⇓
x > -1
3) x > 0
Si studia quindi graficamente il segno della disequazione:
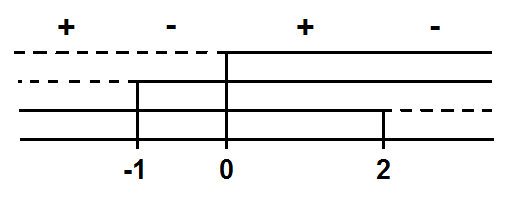
Dalla rappresentazione grafica si deduce che il prodotto di fattori al I membro della disequazione assume valore negativo per -1 < x < 0 oppure per x > 2.
La risposta corretta è, quindi, la b).
Quiz n. 4
Traccia:
In un negozio di abbigliamento Valeria acquista in saldo una gonna che reca come prezzo di listino 40 euro. Se lo sconto applicato è del 30% e se Valeria paga al negoziante con una banconota da 50 euro, quanto riceverà di resto?
a) 20 euro
b) 28 euro
c) 10 euro
d) 15 euro
e) 22 euro
Risoluzione:
Valeria, acquistando la gonna ad un prezzo pari al 70% del prezzo di listino (le viene infatti applicato uno sconto del 30%), deve al negoziante:
Pagando con una banconota da 50 euro, riceverà di resto:
La risposta corretta è, quindi, la e).
Quiz n. 5
Traccia:
Una retta di equazione 2x + y - 3 = 0 interseca l’asse x nel punto P e l’asse y nel punto Q. Qual è la lunghezza del segmento PQ?
a) 9/2
b) 45/4
c) 3√5/2
d) √(21/2)
e) 3√3/2
Risoluzione:
L'ascissa del punto P(x; 0) si ottiene sostituendo il valore y=0 nell'equazione della retta:
⇓
x = 3/2
L'ordinata del punto Q(0; y) si ottiene sostituendo il valore x=0 nell'equazione della retta:
⇓
y = 3
I due punti P(3/2; 0) e Q(0; 3) formano con l'origine degli assi cartesiani O(0; 0) un triangolo rettangolo, la cui ipotenusa coincide proprio con la lunghezza del segmento PQ.
Applicando quindi il teorema di Pitagora al triangolo rettangolo OPQ si ha:
⇓
PQ = √[(3/2)2 + (3)2]
⇓
PQ = √(9/4 + 9)
⇓
PQ = √(45/4)
⇓
PQ = 3√5/2
La risposta corretta è, quindi, la c).
Quiz n. 6
Traccia:
Un gioco per bambini consiste nell’inserire oggetti di diversa forma negli spazi corrispondenti alla forma dell’oggetto. Tra gli oggetti vi sono un rettangolo e un triangolo rettangolo.
- La base del rettangolo è lunga tre volte la sua altezza.
- I lati del triangolo a, b, c sono in ordine di lunghezza crescente.
- Il lato a del triangolo è lungo due volte l’altezza del rettangolo.
- Le aree delle due figure sono uguali.
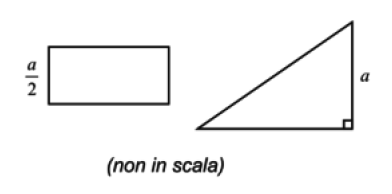
Qual è il rapporto a:b?
a) 3:4
b) 1:3
c) 1:2
d) 1:4
e) 2:3
Risoluzione:
Poiché la base del rettangolo è il triplo della sua altezza si ha:
Coerentemente con le indicazioni fornite dalla traccia del quesito, ai cateti, minore e maggiore del triangolo rettangolo vanno assegnate rispettivamente le lettere "a" e "b"; all'ipotenusa (lato più lungo) va assegnata la lettera "c".
Dato che i due poligoni sono equivalenti, si possono eguagliare l'area del rettangolo e l'area del triangolo ed ottenere quindi il rapporto incognito a/b:
⇓
[(3/2)a]•(a/2) = (b•a)/2
⇓
(3/4)•a2 = (b•a)/2
⇓
(3/4)•a = b/2
⇓
a/b = 4/6 = 2/3
La risposta corretta è, quindi, la e).
Quiz n. 7
Traccia:
Trovare l’equazione della retta passante per i punti (2 , 5) e (6 , –1).
a) 3y + 2x = 16
b) 2y + 3x = 16
c) 2y = 3x − 20
d) 3y = 2x − 15
e) 2y = 3x + 4
Risoluzione:
In geometria analitica, l'equazione della retta passante per due punti di coordinate (x1, y1) e (x2, y2) si calcola mediante la seguente formula:
Applicando tale formula al caso in esame, ed indicando con x1 = 2; y1 = 5; x2 = 6; y2 = -1, si ha:
⇓
-3/2 = (y - 5) / (x - 2)
⇓
-3x + 6 = 2y - 10
⇓
2y + 3x = 16
La risposta corretta è, quindi, la b).
Quiz n. 8
Traccia:
Il triangolo ABC ha un angolo retto nel vertice C. La lunghezza del lato AC è di 5 cm. L’ampiezza dell’angolo CAB è di 60°. Viene tracciato un segmento dal vertice C fino ad intersecare nel punto H il lato AB, in modo che CHB risulti essere un triangolo rettangolo. Qual è la lunghezza in centimetri del segmento HB?
a) 10
b) 2,5
c) 5√3/2
d) 7,5
e) 5√3
Risoluzione:
Nella figura sotto riportata si riportano tutte le indicazioni geometriche fornite dalla traccia dell'esercizio e si indica con "x" la misura incognita del segmento HB.
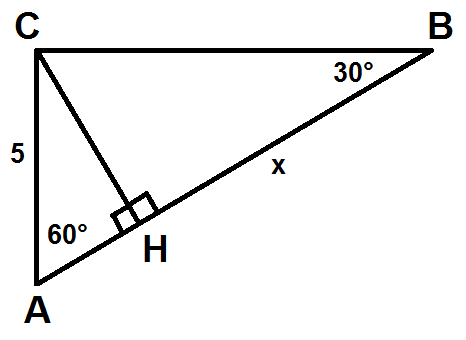
Considerando il triangolo rettangolo AHC si possono trovare le lunghezze dei segmenti AH e CH utilizzando i teoremi sui triangoli rettangoli.
Poichè in un triangolo rettangolo un cateto è uguale al prodotto dell'ipotenusa per il seno dell'angolo opposto, si ha:
⇓
CH = 5 • (√3/2) = (5√3)/2
Inoltre, dato che in un triangolo rettangolo un cateto è anche uguale al prodotto dell'ipotenusa per il coseno dell'angolo adiacente, si ha:
⇓
AH = 5 • (1/2) = 5/2
Per il II Teorema di Euclide il quadrato della misura dell'altezza è uguale al prodotto delle misure delle proiezioni dei cateti sull'ipotenusa.
Si ha quindi:
⇓
[(5√3)/2]2 = (5/2) • x
⇓
75/4 = (5x)/2
⇓
75 = 10x
⇓
x = 7,5 cm
La risposta corretta è, quindi, la d).
Quiz n. 9
Traccia:
La massa media di 4 vogatori è di 85 kg. Uno dei vogatori con una massa di 86 kg si è infortunato ed è stato sostituito. La nuova media aritmetica della massa è di 87 kg. Qual è la massa del nuovo vogatore in kg?
a) 94
b) 86
c) 88
d) 104
e) 90
Risoluzione:
Se la massa media dei 4 vogatori era 85 Kg ed uno di massa 86 kg si è infortunato, si può ipotizzare che siano rimasti 3 vogatori di cui 2 di massa 85 kg (come la media) ed 1 di massa 84 kg (che compensava il vogatore di massa 86 kg nella formazione iniziale).
Si applica quindi la formula della media aritmetica semplice indicando con "x" la massa incognita del nuovo navigatore:
⇓
254 + x = 348
⇓
x = 94 kg
La risposta corretta è, quindi, la a).
Quiz n. 10
Traccia:
Si consideri una circonferenza inscritta in un quadrato. Un rettangolo di base 2 cm ed altezza 1 cm viene inserito nello spazio tra uno dei vertici del quadrato e la circonferenza in modo tale che un vertice del rettangolo coincida con quello del quadrato ed il vertice opposto giaccia sulla circonferenza.
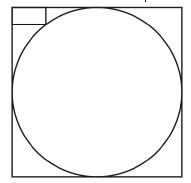
Calcolare il raggio della circonferenza.
a) √2 cm
b) √5 cm
c) 5 cm
d) 2 cm
e) √2/(√2 - 1) cm
Risoluzione:
Nella figura sotto riportata si indica con O il centro della circonferenza e si indicano con A, B e C gli estremi di 3 raggi della circonferenza stessa.
Si ha quindi OA = OB = OC = r.
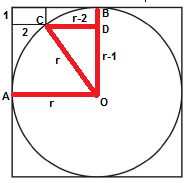
Poichè, per ipotesi, le dimensioni del rettangolo sono 2 cm (base) e 1 cm (altezza), si ricavano le lunghezze dei segmenti OD e CD:
CD = OA - 2 = r -2
Si applica quindi il teorema di Pitagora al triangolo rettangolo OCD in cui OD e CD, appena calcolati, sono i cateti, mentre OA (raggio) è l'ipotenusa:
⇓
r2 = (r-2)2 +(r-1)2
⇓
r2 = r2 - 4r + 4 + r2 - 2r + 1
⇓
r2 - 6r + 5 = 0
⇓
Δ/4 = 4
⇓
r = 1 cm (non accettabile) o r = 5 cm
La risposta corretta è, quindi, la c).
LEZIONI PRIVATE ONLINE con l'Ing. Galeone
Ti stai preparando per il Test di ammissione alla Facoltà di Archiettura?
Affidati alla professionalità e all'esperienza...acquista ora la tua lezione privata online, via Skype, con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!