In questa pagina si riportano 5 esercizi svolti di Statistica utili per prepararsi all'esame di Statistica - I anno corso di laurea facoltà di Medicina e Chirurgia - Università San Raffaele.
Esercizio n. 1 (indice chi quadrato)
Traccia:
Nel corso di una ricerca vengono intervistati ragazzi e ragazze a cui viene richiesto il tipo di sport praticato. In base ai dati raccolti (vedi tabella), calcolare l'indice chi quadrato per verificare se il tipo di sport è associato o meno al sesso dei ragazzi.
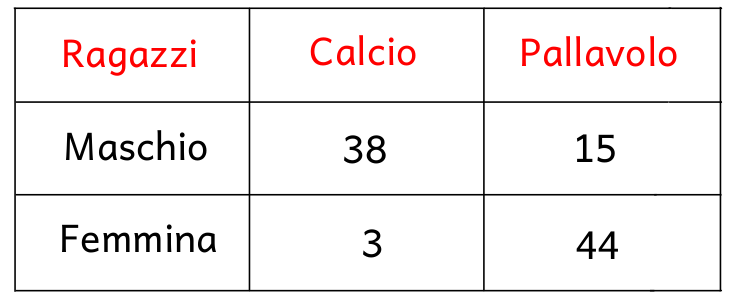
Risoluzione:
Si completa dapprima la tabella delle frequenze assolute osservate fornita dalla traccia del quesito riportando i totali di riga e di colonna:
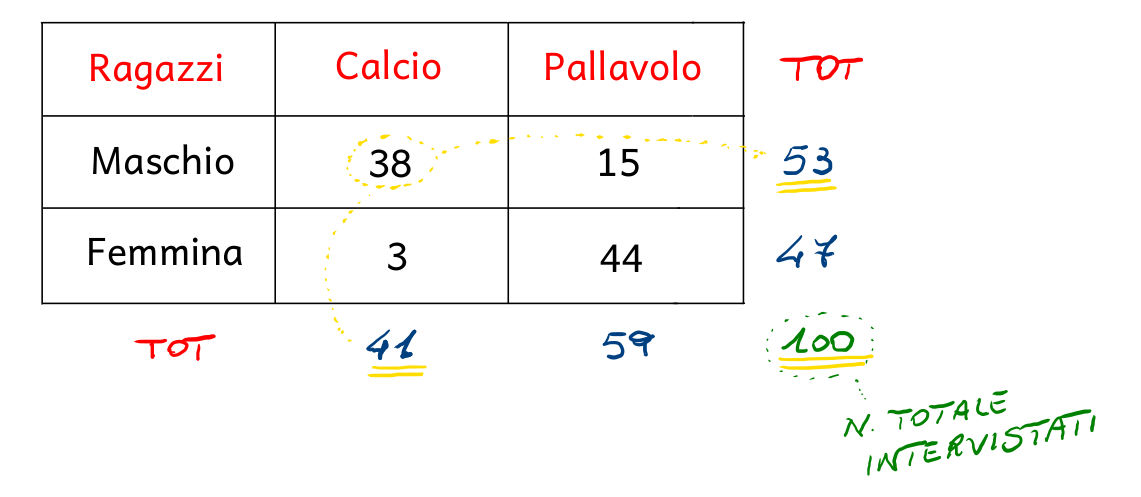
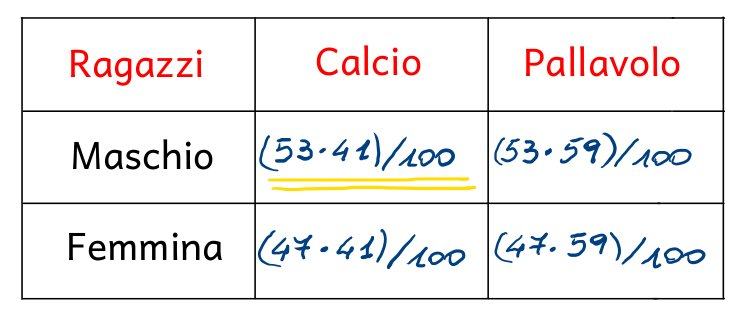
Svolgendo i calcoli, i valori delle frequenze assolute attese sono i seguenti:
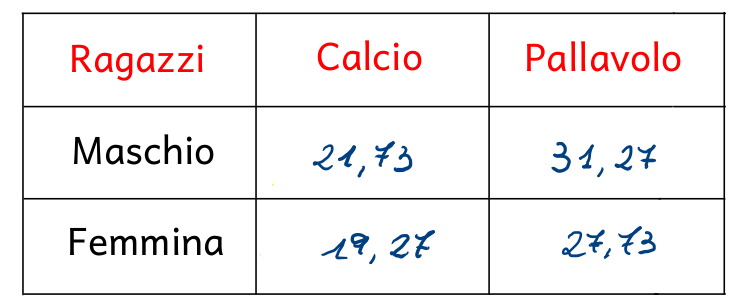
Facendo riferimento alle tabelle delle frequenze assolute osservate e delle frequenze assolute attese, la formula per calcolare l'indice chi quadrato è la seguente:
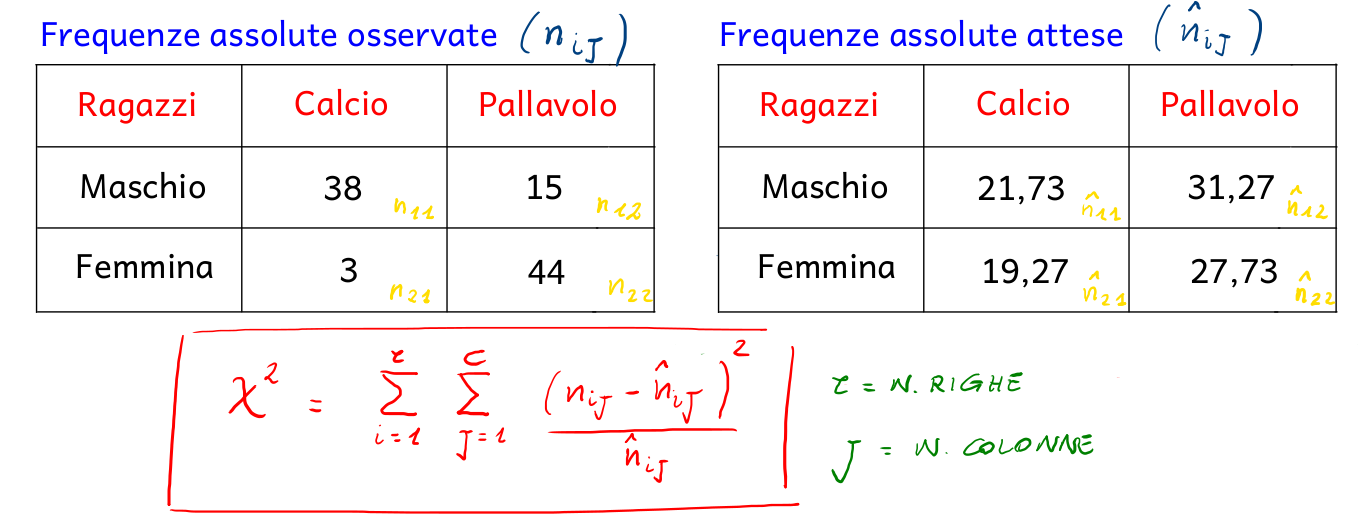
Applicando la formula precedente al caso in esame, si ottiene il valore dell'indice chi quadrato:
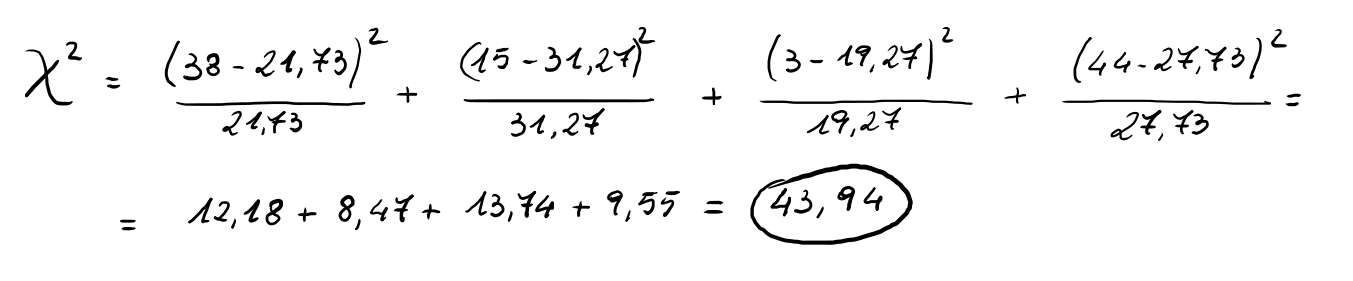
Poichè il valore dell'indice chi quadrato non è prossimo allo zero, le due variabili "tipo di sport" e "sesso dei ragazzi" sono sicuramente associate.
Esercizio n. 2 (test diagnostico)
Traccia:
Viene condotto uno studio per valutare un nuovo test per diagnosticare il tumore al cervello. Per lo studio vengono reclutati 1.000 individui, di cui 450 malati e 550 sani. I risultati dello studio sono riportati nella tabella di seguito:
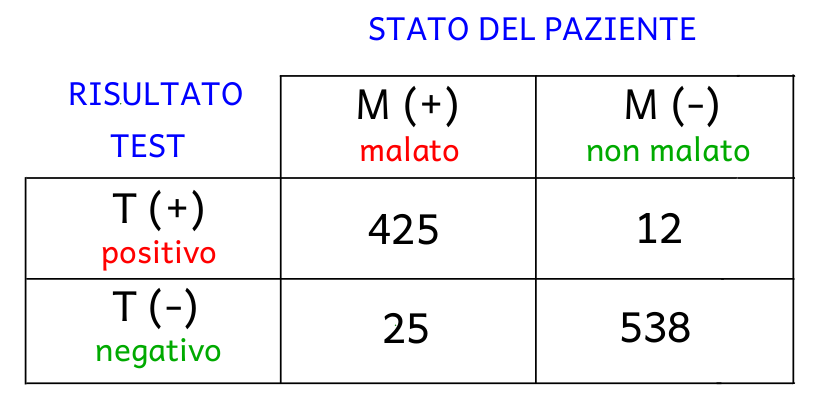
Calcolare sensibilità e specificità del test diagnostico.
Risoluzione:
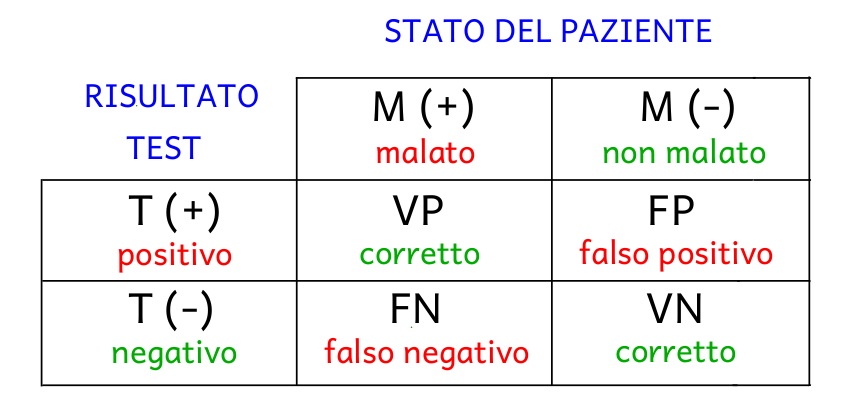
Data una tabella di contingenza 2x2 relativa ad un test diagnostico, si possono identificare le seguenti quantità:
- veri positivi (VP): numero di individui malati e positivi al test;
- falsi positivi (FP): numero di individui sani (non malati) e positivi al test;
- veri negativi (VN): numero di individui sani (non malati e negativi al test;
- falsi negativi (FN): numero di individui malati e negativi al test.
Nel caso in esame, alle quantità sopra indicate, si possono associare i seguenti valori:
VP = 425;
FP = 12;
FN = 25;
VN = 538.
La sensibilità di un test diagnostico può essere calcolata mediante la seguente formula:
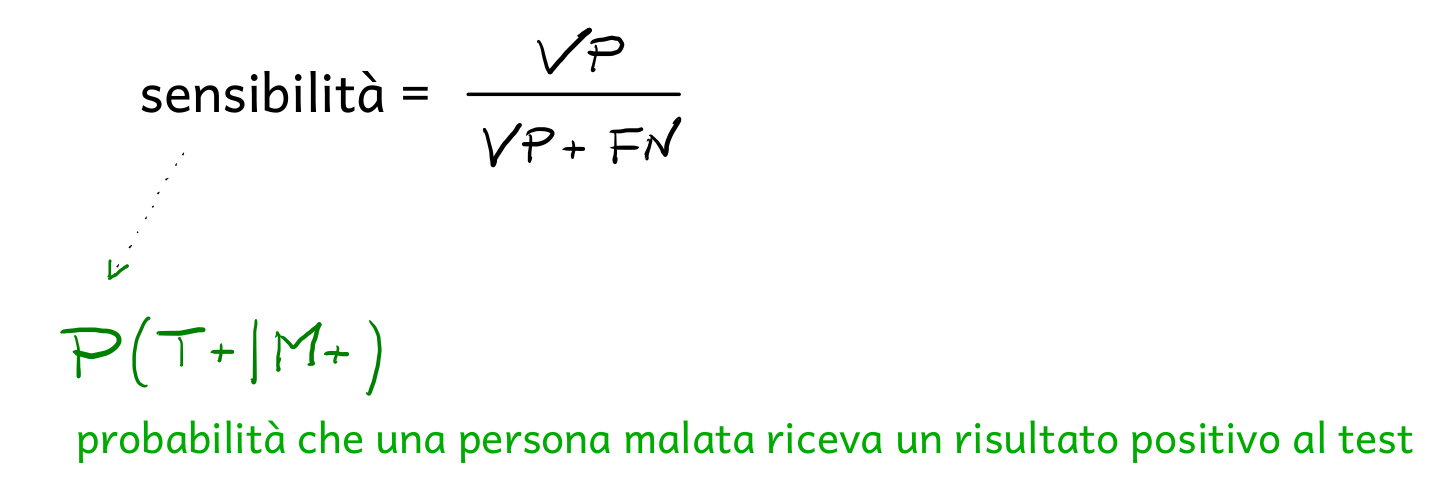
Applicando la formula precedente al caso in esame, si ottiene il valore della sensibilità:
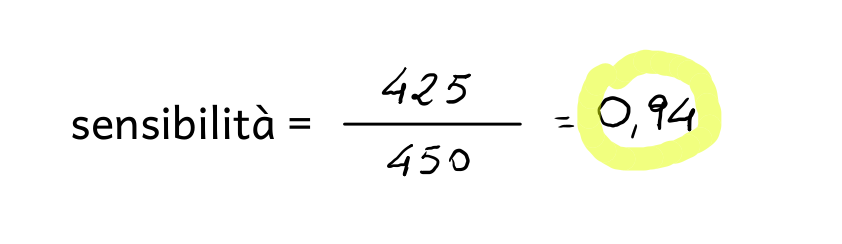
La specificità di un test diagnostico indica, invece, la probabilità che una persona sana (non malata) riceva un risultato negativo al test e può essere calcolata mediante la seguente formula:

Applicando la formula precedente al caso in esame, si ottiene il valore della specificità:
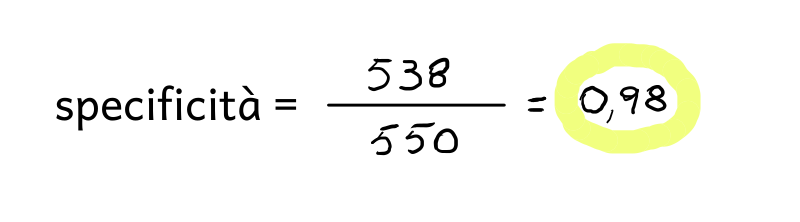
Entrambi i valori di sensibilità e specificità sono prossimi all'unità (in termini percentuali, probabilità del 94% e del 98% rispettivamente). Si deduce che il test diagnostico risulta essere molto accurato.
LEZIONI PRIVATE ONLINE CON L'ING. GALEONE
Ti stai preparando per l'esame di Statistica presso la facoltà di Medicina dell'Università San Raffaele?
Prenota ora la tua lezione privata online con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!
Per maggiori info contatta l'Ing. Galeone al numero di cellulare 3384610628, anche su WhatsApp.
Esercizio n. 3 (covarianza e coefficiente di correlazione lineare)
Traccia:
Nella tabella seguente vengono raccolti i dati dell'età (variabile X) e dei valori di colesterolo nel sangue (variabile Y) di 8 individui:

Calcolare la covarianza e il coefficiente di correlazione lineare tra le 2 variabili.
Risoluzione:
La covarianza (SXY) misura come due variabili quantitative X e Y si discostano dai loro valori medi. E' quindi un indicatore sintetico sulla variazione contemporanea dei valori di due variabili quantitative.
La formula per calcolare la covarianza è la seguente:
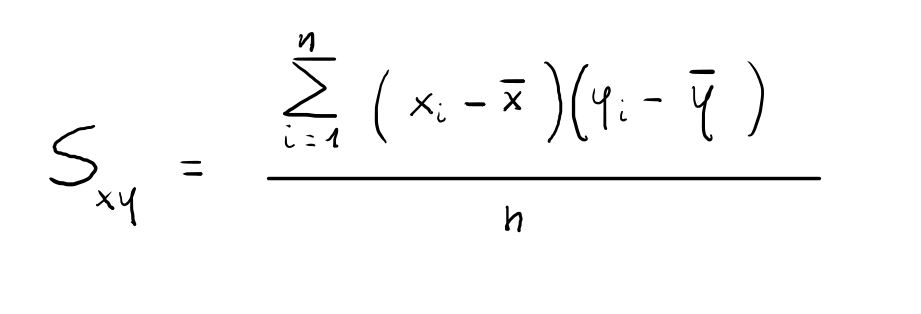
In alternativa può essere utilizzata un'altra formula, sicuramente più "pratica":
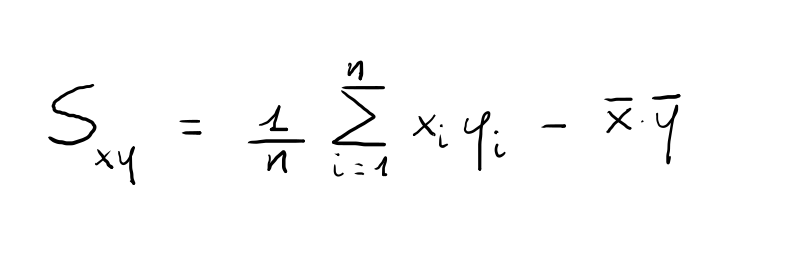
La covarianza misura il segno della relazione lineare tra le due variabili:
- SXY > 0 ⇒ X e Y sono direttamente correlate, pertanto al crescere di X, cresce anche Y;
- SXY = 0 ⇒ X e Y non sono lineramente correlate;
- SXY < 0 ⇒ X e Y sono inversamente correlate, pertanto al crescere di X, Y decresce.
Volendo usare la formula "pratica", si procede al calcolo delle singole quantità necessarie al calcolo della covarianza:
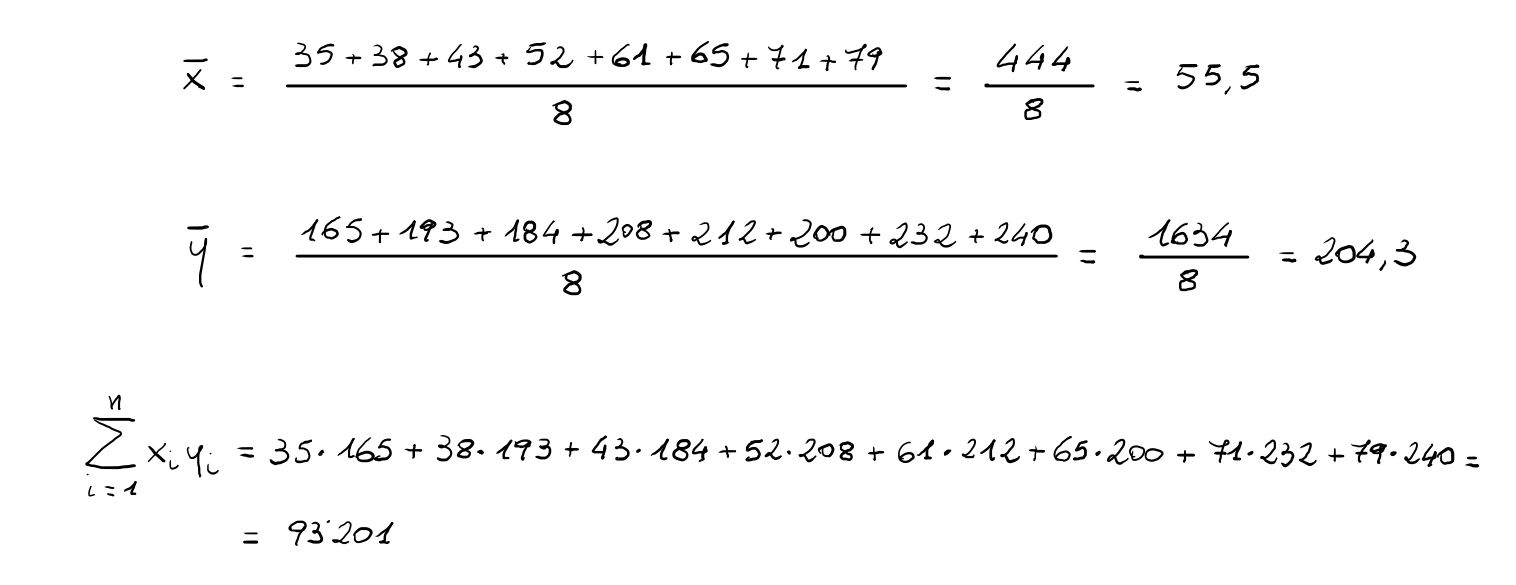
Si riesce quindi a determinare il valore della covarianza relativa alle due variabili X (età) e Y (valore colesterolo):
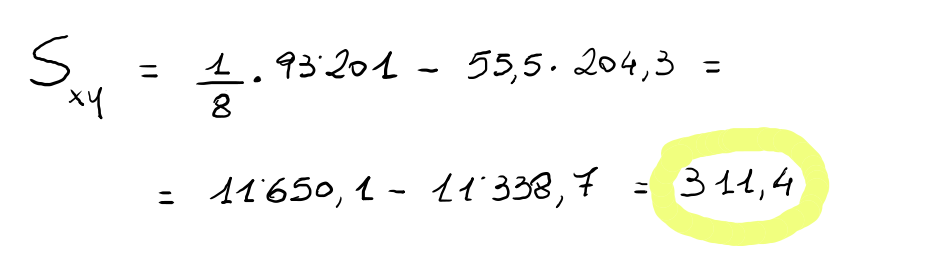
Poichè il valore della covarianza è positivo, le due variabili sono direttamente correlate, cioè al crescere dell'età crescono anche i valori del colesterolo nel sangue.
Il coefficiente di correlazione lineare di Pearson (ρXY) non solo fornisce un'indicazione sulla direzione della relazione lineare (diretta o inversa) tra due variabili quantitative X e Y (come la covarianza), ma indica anche quanto è forte la relazione lineare (se esiste) fra X e Y.
La formula per calcolare il coefficiente di correlazione lineare di Pearson è la seguente:
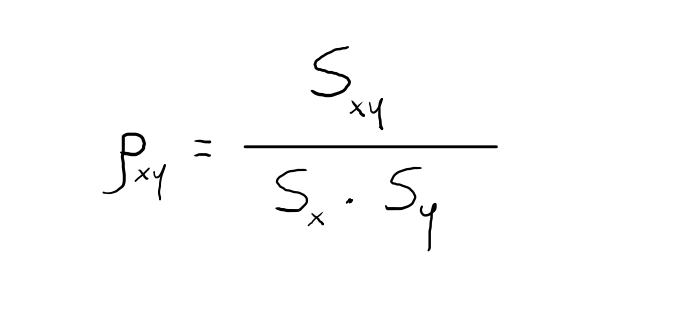
dove Sx e Sy indicano i valori delle deviazioni standard delle variabili X e Y.
Il coefficiente di correlazione lineare ρXY è sempre compreso tra -1 e 1 e, in base ai suoi valori, possono essere fatte le seguenti considerazioni:
- ρXY > 0 ⇒ X e Y sono direttamente correlate, pertanto al crescere di X, cresce anche Y; quanto più ρXY è vicino a 1, tanto più è forte la relazione lineare positiva.
- ρXY = 0 ⇒ X e Y non sono lineramente correlate;
- ρXY < 0 ⇒ X e Y sono inversamente correlate, pertanto al crescere di X, Y decresce; quanto più ρXY è vicino a -1, tanto più è forte la relazione lineare negativa.
Si procede al calcolo delle deviazioni standard delle variabili X e Y:
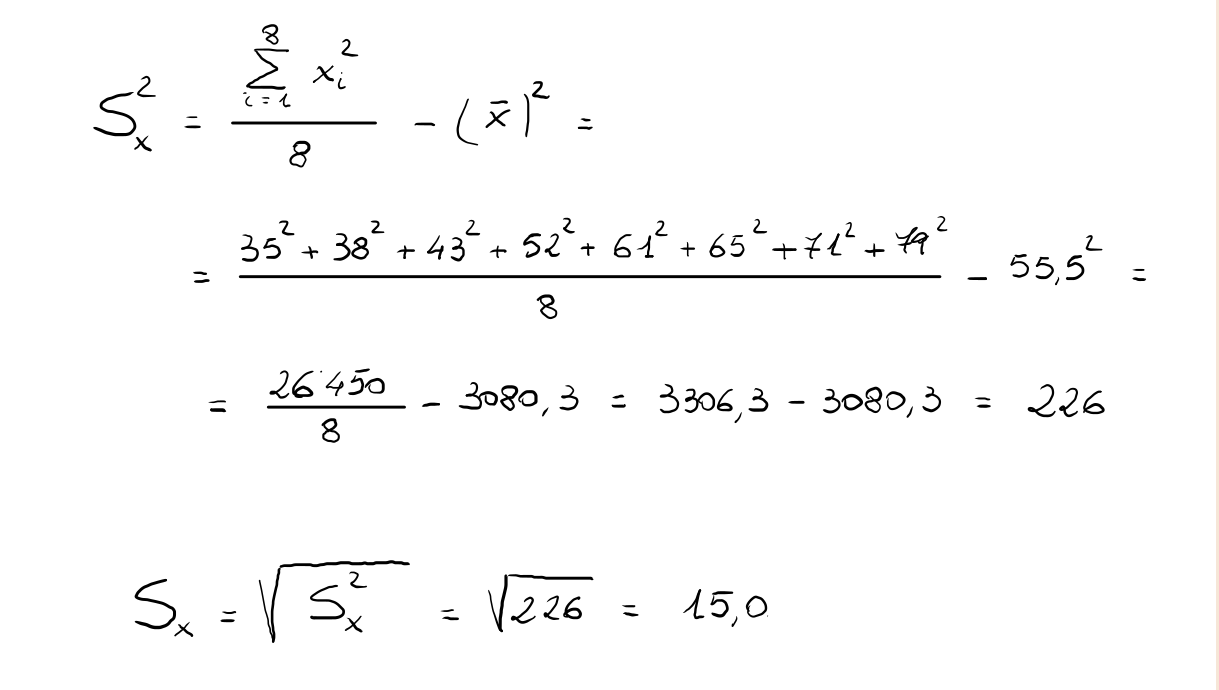
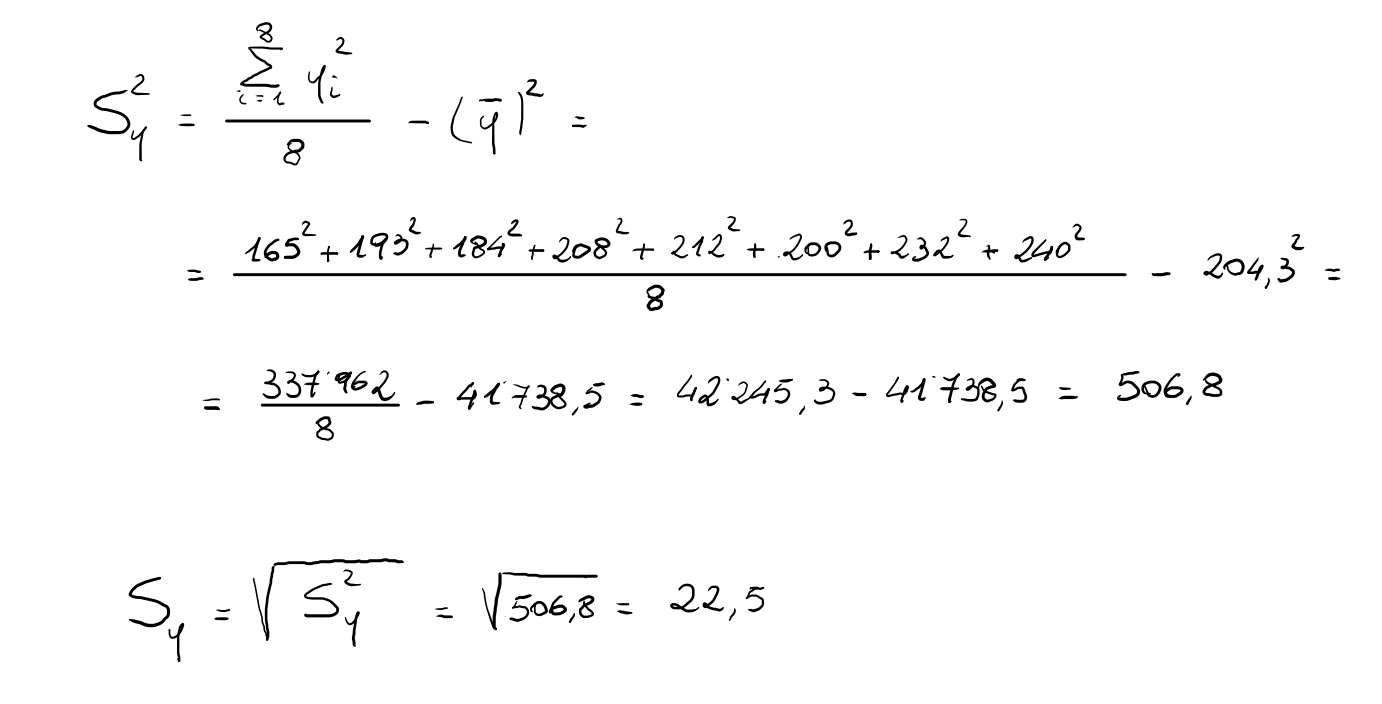
Si riesce quindi a determinare il valore del coefficiente di correlazione lineare ρxy:
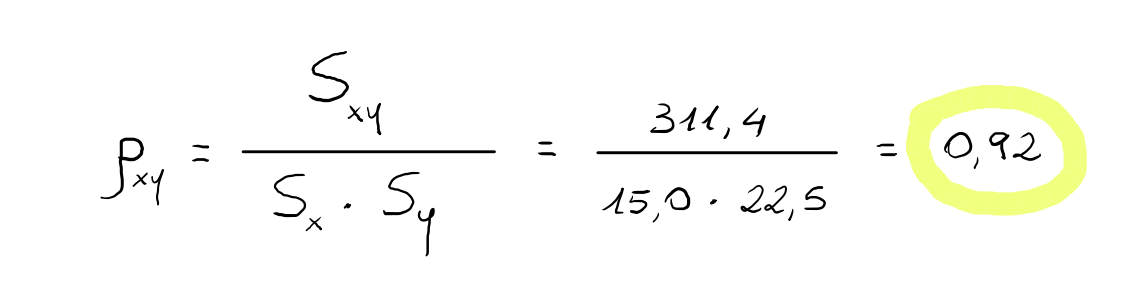
Poichè il valore del coefficiente di correlazione lineare è positivo, le due variabili sono direttamente correlate, cioè al crescere dell'età crescono anche i valori del colesterolo nel sangue. Inoltre, essendo il valore di ρxy molto vicino a 1, la relazione lineare positiva è molto forte.
Esercizio n. 4 (distribuzione di Poisson)
Traccia:
Un negozio di forniture sanitarie vende mediamente 5 aspiratori chirurgici a settimana.
(a) Qual è la probabilità che ne venda almeno 2 a settimana?
(b) Ipotizzando che i giorni lavorativi a settimana siano 6, qual è la probabilità che il negozio in un determinato giorno venda esattamente 2 aspiratori chirurgici?
Risoluzione:
Nel caso in esame, per calcolare le probabilità richieste si può fare riferimento alla distribuzione di Poisson.
La distribuzione di Poisson è una distribuzione di probabilità discreta che si applica quando si vuole conoscere la probabilità che un evento si verifichi "x" volte in un determinato intervallo continuo di spazio o di tempo, sapendo che mediamente esso si verifica "λ" volte.
La formula per calcolare la probabilità è la seguente:
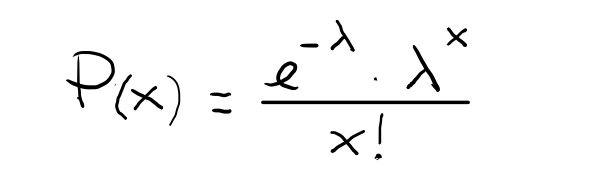
dove:
- x = numero di eventi per intervallo di spazio o tempo di cui si vuole conoscere la probabilità;
- λ = numero medio di eventi nell'intervallo di spazio o di tempo considerato;
- e = numero di Nepero = 2,7182...
Per calcolare la probabilità che il negozio di forniture sanitarie venda 2 o più aspiratori chirurgici, si deve fare riferimento alle tavole statistiche di Poisson.
Tali tavole riportano la funzione di ripartizione (o funzione cumulativa) di una variabile aleatoria X che esprime (in funzione del parametro λ sopra definito) la probabilità che la variabile X assuma valori minori o uguale ad un generico valore x0:
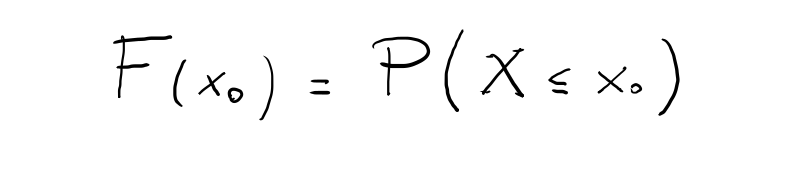
Tenendo conto della regola per calcolare la probabilità del complementare di un evento, la probabilità che il negozio di forniture sanitarie venda 2 o più aspiratori chirurgici si può ricavare nel seguente modo:
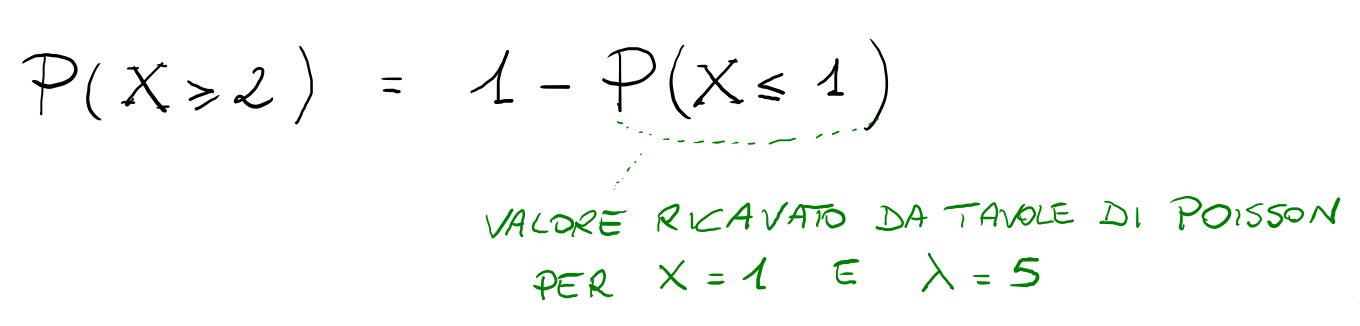
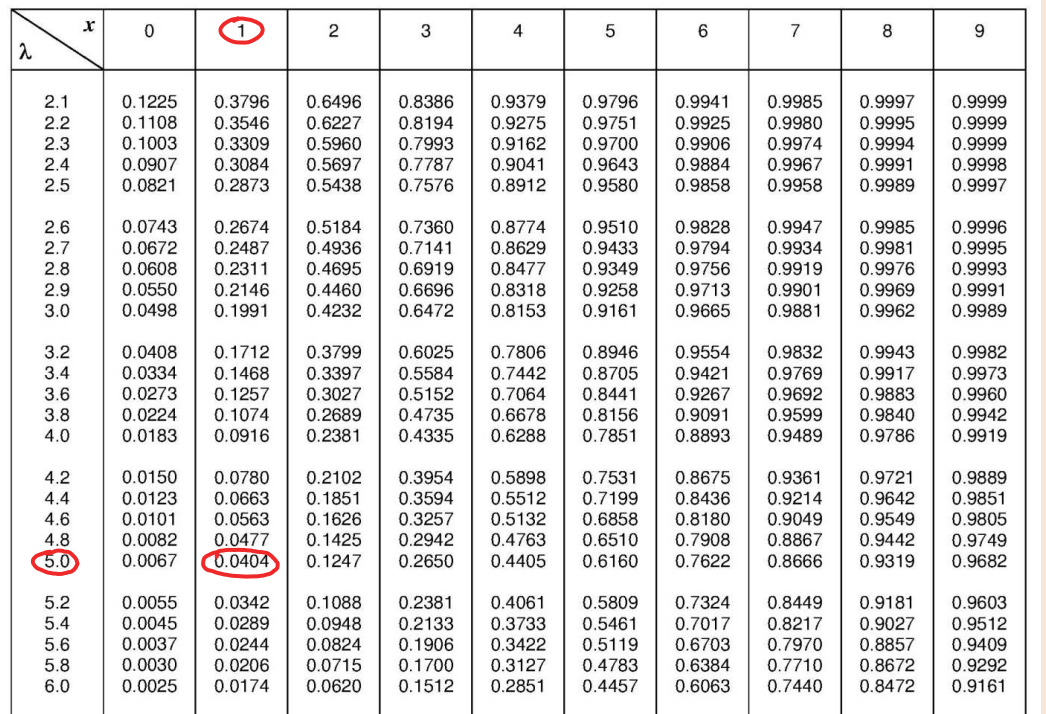
Dalle tavole di Poisson sotto riportate si ottiene, quindi, il risultato finale richiesto dal punto (a):
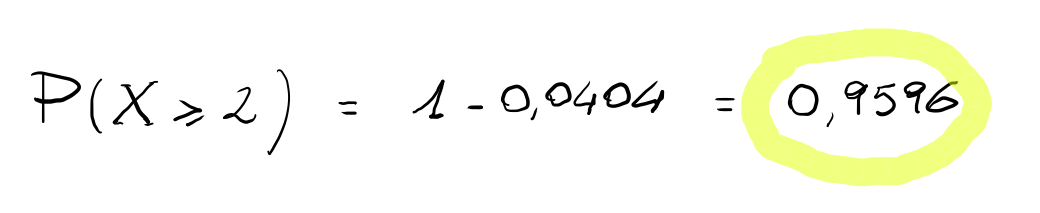
Pertanto, un negozio di forniture sanitarie, che vende mediamente 5 aspiratori chirurgici a settimana, ha la probabilità del 95,96% di venderne almeno 2 in una settimana.
Si vuole ora calcolare la probabilità che il negozio di forniture sanitarie in un determinato giorno venda esattamente 2 aspiratori chirurgici, tenendo presente che vengono venduti mediamente 5 aspiratori chirurgici a settimana e che i giorni lavorativi a settimana siano 6.
Riprendendo la formula per calcolare la probabilità in una distribuzione di Poisson:
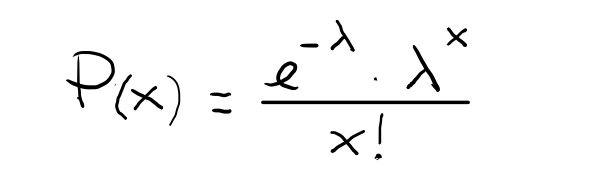
dove nel caso in esame:
- x = numero di aspiratori chirurgici venduti in un giorno;
- λ = numero medio di aspiratori chirurgici venduti in un giorno = 5/6;
- e = numero di Nepero = 2,7182...
Calcolando la probabilità richiesta si ha:
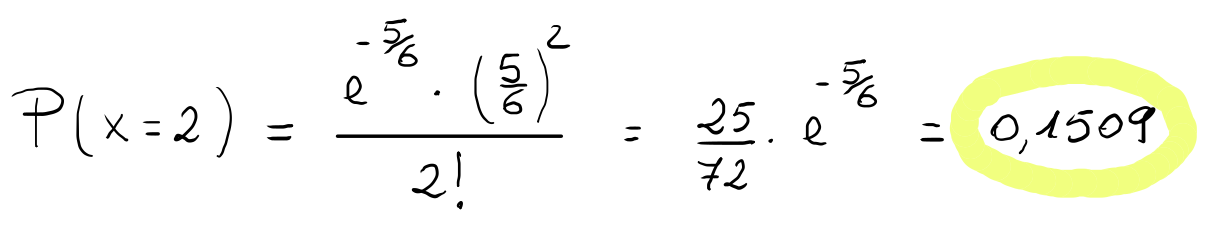
Si deduce quindi che il negozio di forniture sanitarie, che mediamente vende 5 aspiratori chirurgici a settimana e lavora 6 giorni a settimana, ha la probabilità del 15.09% di vendere esattamente 2 aspiratori chirurgici in un determinato giorno.
Esercizio n. 5 (distribuzione Normale)
Traccia:
All'esame di Fisica i voti conseguiti dagli studenti iscritti al I anno della facoltà di Medicina e Chirurgia hanno media 26 e varianza 4. Supponendo che i voti (variabile X) abbiano distribuzione normale, determinare:
(a) il valore della variabile standardizzata (Z-score) per il voto 24;
(b) la probabilità che il voto assegnato dalla commissione d'esame sia almeno 24.
Risoluzione:
La distribuzione normale standard (generalmente indicata con Z) è una distribuzione normale (indicata invece con la N) con media 0 e varianza 1:
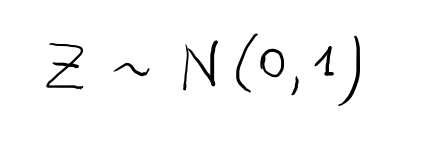
Si consideri una variabile aleatoria normale X con media "μ" e varianza "σ2":
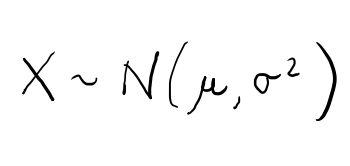
E' possibile trasformare la variabile X nella variabile Z sottraendo a X la sua media (μ) e dividendo per la sua deviazione standard (σ):
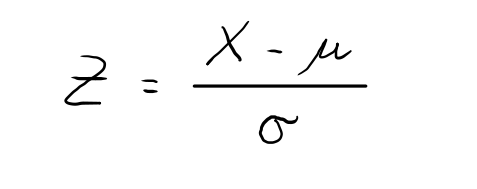
Nel caso in esame si ha:
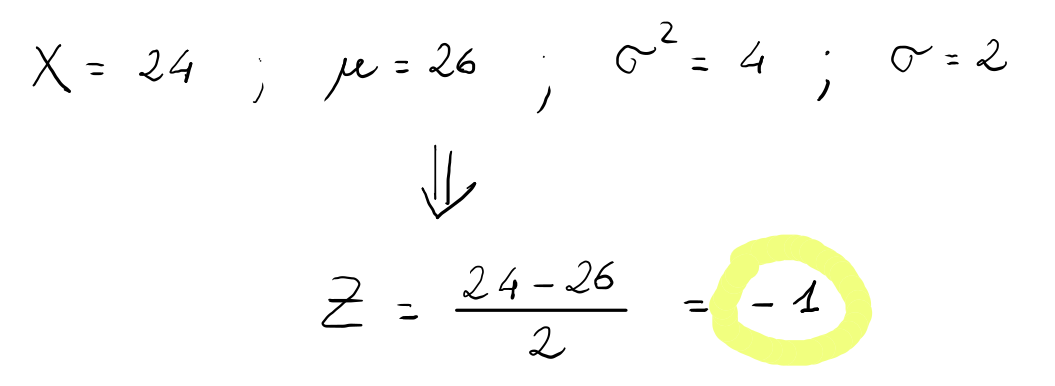
Pertanto, il valore della variabile standardizzata (Z-score) per il voto 24 è -1.
Relativamente al caso studiato, la distribuzione normale e la distribuzione normale standard possono essere così rappresentate:
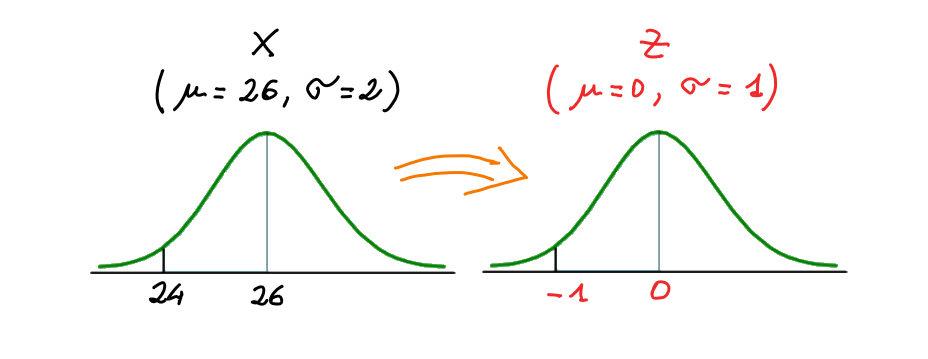
Passando al punto (b), il quesito richiede di calcolare la probabilità che il voto assegnato dalla commissione sia almeno 24, ossia P(X>=24). Dall'immagine sottostante si può notare come il valore della probabilità richiesta (area colorata in giallo sottesa al grafico della funzione cumulativa) sia la stessa e sia cambiata solo la scala di rappresentazione:
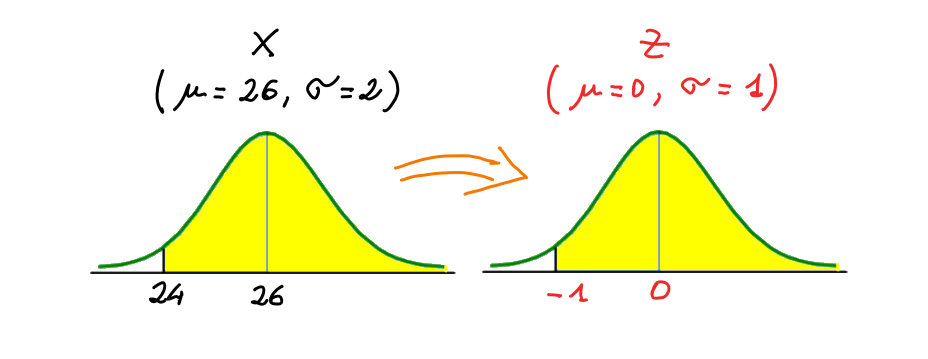
Pertanto, potendo formulare il problema utilizzando in maniera equivalente o le unità originali (X) o le unità standardizzate (Z), per calcolare la probabilità richiesta è sufficiente fare riferimento alle sole tavole statistiche della distribuzione normale standard:
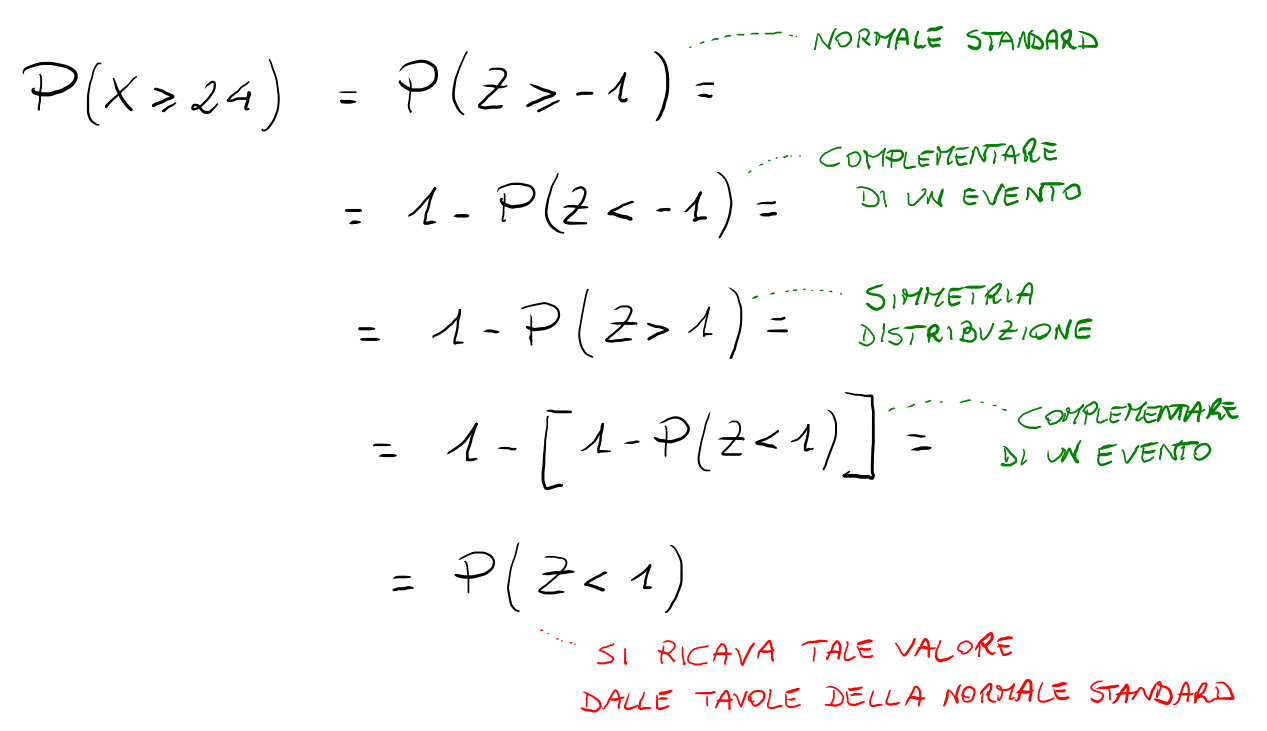
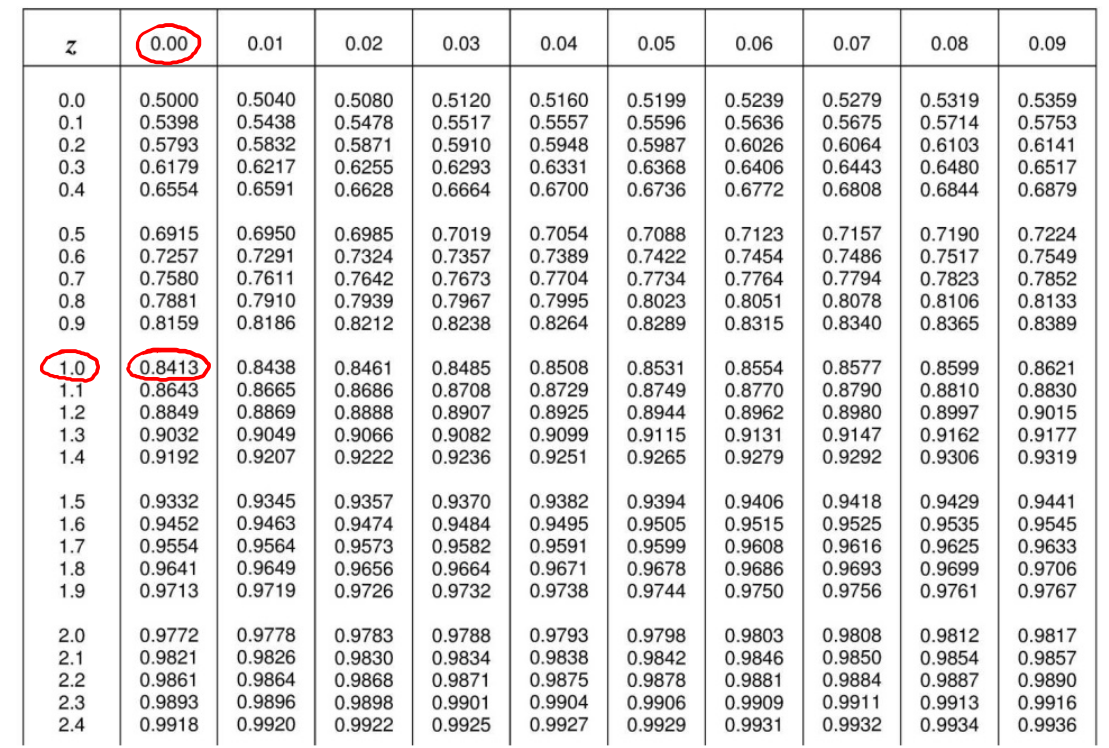
In definitiva si ha che:
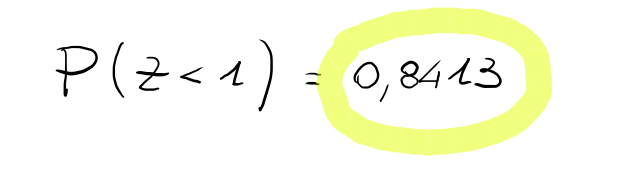
La probabilità che uno studente all'esame di Fisica ottenga un voto uguale o maggiore a 24 è dell'84,13%.
LEZIONI PRIVATE ONLINE CON L'ING. GALEONE
Ti stai preparando per l'esame di Statistica presso la facoltà di Medicina dell'Università San Raffaele?
Prenota ora la tua lezione privata online con l'Ing. Galeone.
Le lezioni saranno individuali e altamente personalizzate...così avrai un aiuto mirato alle tue specifiche esigenze formative!
Per maggiori info contatta l'Ing. Galeone al numero di cellulare 3384610628, anche su WhatsApp.